Jeffrey M. Hokanson

The Lipschitz matrix generalizes the notion of Lipschitz continuity by pulling the scalar Lipschitz constant inside the norm, promoting it to a matrix. Whereas a scalar Lipschitz function $ f\in \set L(\set D, L)$ satisfies $$ \set L(\set D, L) := \lbrace f:\set D\to \R: |f(\ve x_1) - f(\ve x_2) | \le L\| \ve x_1 - \ve x_2\|_2 \ \forall \ve x_1, \ve x_2 \in \set D \rbrace, $$ a matrix Lipschitz function $f\in \set L(\set D, \ma L)$ satisfies $$ \set L(\set D, \ma L) := \lbrace f:\set D\to \R: |f(\ve x_1) - f(\ve x_2) | \le \|\ma L( \ve x_1 - \ve x_2)\|_2 \ \forall \ve x_1, \ve x_2 \in \set D\rbrace. $$ In this manuscript we show that we can estimate the Lipschitz matrix from both samples $f(\widehat{\ve x}_j)$ and gradients $\nabla f(\check{\ve x}_k)$ using a semidefinite program. The Lipschitz matrix can then be used to estimate the active subspace of a function much like the average outer product of gradients. Moreover the Lipschitz matrix provides tighter bounds on the uncertainty in the function, motivates a space filling design of experiments, and can reduce the worst-case information based complexity of approximation, integration, and optimization compared to the scalar Lipschitz case.

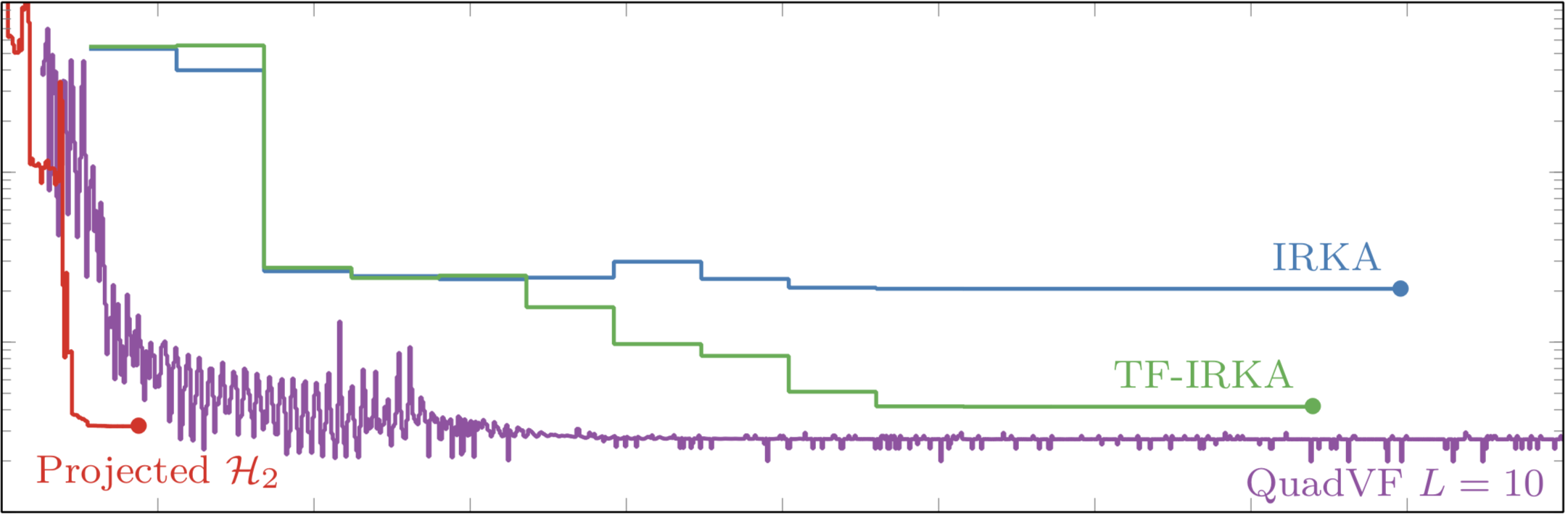
Given access to the transfer function of a linear time-invariant system $H$, model reduction seeks to construct a reduced order model $H_r$ that emulates the dynamics of the full order model. Commonly these reduced order models are choosen to have a real, stable, finite-dimensional state-space form and hence their transfer functions are proper rational functions of degree $r$ whose poles are in the left-half plane; i.e., $H_r \in \mathcal{R}_r(\mathbb{R})^+$. $\mathcal{H}_2$-optimal model reduction seeks the reduce order model that minimizes the $\mathcal{H}_2$-norm: $$ \min_{H_r\in \mathcal{R}_r^+(\mathbb{R})} \| H - H_r \|_{\mathcal{H}_2}^2, \qquad \| F \|_{\mathcal{H}_2}^2 = \int_{-\infty}^\infty |F(i\omega)|^2 \mathrm{d}\omega. $$ By exploiting the Hilbert space structure of this norm, we are able to construct an efficient algorithm that solves the $\mathcal{H}_2$-optimal model order reduction problem by projecting onto a sequence of finite dimensional subspaces, each yielding a least squares rational approximation problem $$ H_r^{\ve\mu^{(k)}} = \argmin_{H_r\in \mathcal{R}_r^+(\mathbb{R})} \| P(\ve\mu_k) [H - H_r]\|_{\mathcal{H}_2}^2. $$

Given measurements of a linear time-invariant system, the McMillan degree is the dimension of the smallest such system that reproduces these observed dynamics. When given impulse response measurements $\lbrace y_j \rbrace_{j=0}^{n-1}$ of the system $\lbrace \ma A, \ve c, \ve x_0\rbrace$, $$ y_j := \ve c^* \ve x_j \quad \ve x_{j+1} := \ma A \ve x_j $$ the McMillan degree is the rank of the Hankel matrix $\ma H$ built from $\lbrace y_j \rbrace_{j=0}^{n-1}$: $$ \ma H = \begin{bmatrix} y_0 & y_1 & \cdots & y_{m-1} \\ y_1 & y_2 & \cdots & y_m \\ \vdots &\vdots & & \vdots \\ y_{n-m-1} & y_{n-m} &\cdots & y_{n-1} \end{bmatrix}. $$ However if $\lbrace y_j \rbrace_{j=0}^{n-1}$ is contaminated by noise, this matrix is almost surely full rank. In this paper we introduce a new upper bound on the rank of a random Hankel matrix and use this bound to construct a lower bound of the McMillan degree.

A ridge approximation mimics a scalar function of many variables $f: \R^m\to \R$ by another function $g:\R^n \to \R$ of a few linear combinations of inputs such that $$ f(\ve x) \approx g(\ma U^\trans \ve x) \quad \ma U\in \R^{m\times n} \quad \ma U^\trans \ma U = \ma I. $$ In this paper we find the ridge function $g$ and the subspace spanned by $\ma U$ by minimizing the 2-norm mismatch between $f(\ve x_i)$ and $g(\ma U^\trans \ve x_i)$ over a user provided set of points $\lbrace \ve x_i\rbrace_{i=1}^N$. By assuming $g$ is a multidimensional polynomial, we can implicitly solve for the coefficients using variable projection and solve the remaining optimization problem over the Grassmann manifold of $n$-dimensional subspaces of $\R^m$. The resulting algorithm allows for the rapid construction of ridge approximations using only function values.

The exponential fitting problem seeks to minimize the mismatch between a noisy vector of measurements $\tve y\in \R^n$ and a sum of complex exponentials in a least squares sense: $$ \minimize_{\ve \omega, \ve a\in \C^p} \| \ve f(\ve\omega, \ve a) - \tve y\|_2^2 \qquad [\ve f(\ve\omega, \ve a)]_k = \sum_{j=1}^p a_j e^{\omega_j k}. $$ To speed optimization when vast quantities of data are present, we project the problem onto a low dimensional subspace $$ \|\ma W \ma W^*\ve f(\ve\omega, \ve a) - \ma W^*\tve y\|_2^2= \|\ma W^*\ve f(\ve\omega, \ve a) - \ma W^*\tve y\|_2^2, \quad \ma W^*\ma W = \ma I. $$ By a careful selection of $\ma W$ that allows us to efficiently evaluate $\ma W^*\ve f(\ve\omega, \ve a)$ we are able to outperform subspace-based approaches for exponential fitting.

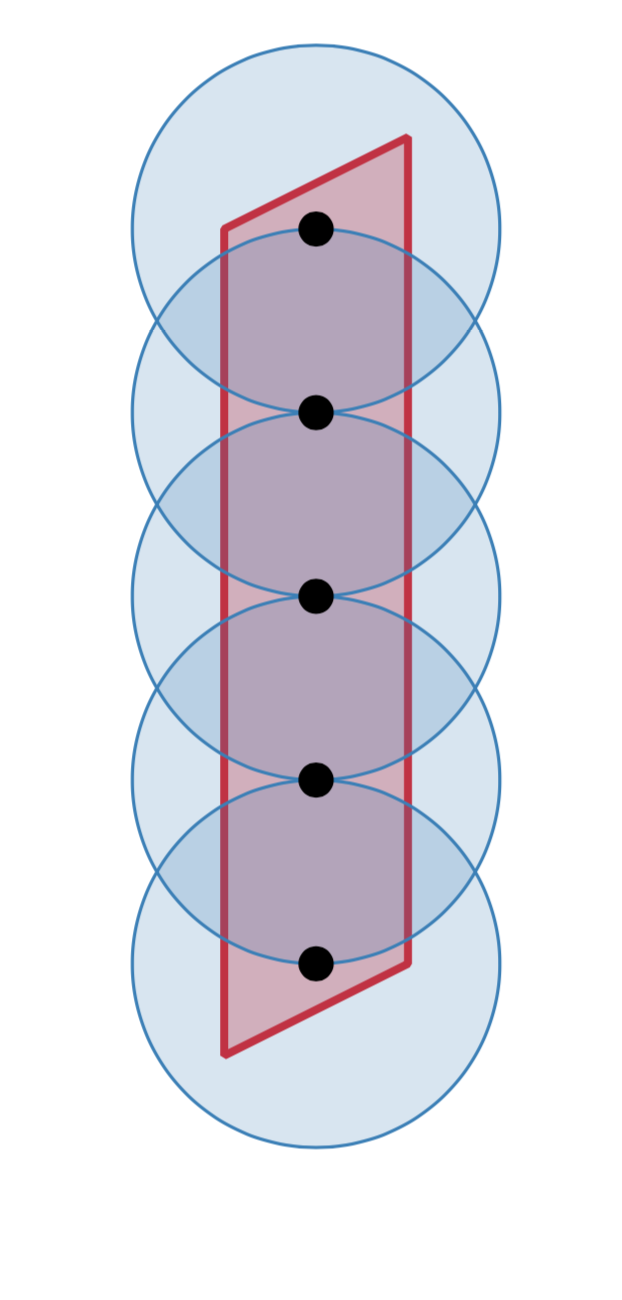
An inverse eigenvalue problem seeks to infer properties of a system through its eigenvalues. A classic example is Kac's question: Can one hear the shape of a drum?; the answer turns out to be no in two dimensions. In this paper we develop a version of this problem accessible to undergraduates in a matrix analysis course. Here we consider the case of a beaded string where the beads are symmetrically distributed around the mid-point of the string. Using classical results of Gantmacher, Krein, and others, we develop an algorithm to recover the masses and locations of these beads given the resonant frequencies of the beaded string. We apply this algorithm to datasets generated from an actual beaded string. This example is used as component of a teaching lab suitable for juniors and above.

The goal of parameter space dimension reduction is to provide a reduced set of coordinates to approximately describe a function. Specifically, given a scalar-valued function $f:\set D \subset \R^m \to \R$, we seek to find a surjective map $h:\set D\to \R^n$ where $n\ll m$ such that $$ f(\ve x) \approx g(h(\ve x)) \quad \forall \ve x \in \set D, \ g:\R^n\to \R.$$ By identifying $h$ mapping to a lower dimensional space, the complexity of approximating $f$ no longer grows exponentially in input dimension $m$. This package includes:

dimension reduction	Lipschitz matrix average outer product of gradients
response surfaces	polynomial ridge approximation Gaussian process
test problems	NACA0012 MULTI-F borehole
domains	linear-quadratic linear-inequality convex hull
function tools	normalization dask-based parallelism

As part of labs 3 and 4, the students would work with a spring network resembling problems in the course textbook. In lab 3, the students would verify the forward problem: knowing the stiffness of the springs, the topology, and the applied loads they would compute the expected displacement and check that it matched the model. In lab 4, the students would solve the inverse problem: knowing the topology of the spring network and the displacements they would attempt to infer stiffness of each spring.

In labs 9 and 10 the students would work with a beaded string. In the first lab, the students would study the forward problem: placing beads on the string knowing their displacement and mass and verify the eigenvalues of the string matched a discrete model In the second lab, the students would place the beads symmetrically around the mid-point of the string and estimate the masses and location of the beads from the measured eigenvalues.